|
Einige Fakten über elliptische Kurven: |
|
Elliptische Kurven sind mathematische Objekte, die bereits seit Jahrzehnten intensiv studiert werden und die einer recht einfach aussehenden Gleichung genügen: E: y^2=x^3+ax+b. Fasst man diese Gleichung über den reellen Zahlen auf, so hat der Graph in der zweidimensionalen Ebene das Aussehen einer Kurve, deren Form von den Parametern a und b abhängt. Die beiden Abbildungen weiter unten zeigen Beispiele solcher Kurven. |
|
Eine interessante Eigenschaft elliptischer Kurven ist es, dass ihre Punkte (das sind diejenigen Punkte aus der Ebene, deren Koordinaten die Kurvengleichung erfüllen) eine Gruppenstruktur aufweisen. Man kann also Punkte addieren und erhält wieder einen Punkt auf der Kurve. Außerdem existiert ein so genannter Punkt im Unendlichen, der die Rolle des neutralen Elements spielt. Will man die Addition auf einer elliptischen Kurve graphisch darstellen, so gibt es eine schöne Methode dafür: man legt eine Gerade durch die beiden Punkte, und diese schneidet die Kurve in genau einem weiteren Punkt (dies ist eine weitere Eigenschaft elliptischer Kurven). Spiegelt man diesen Schnittpunkt an der x-Achse, so erhält man die Summe der beiden Punkte. Dieses Verfahren ist in den beiden Abbildungen unten einmal dargestellt. |
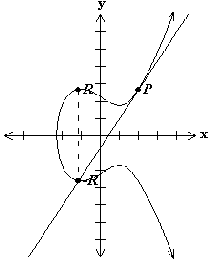
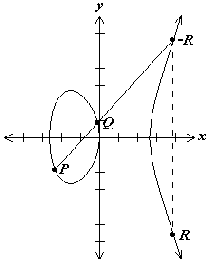
Illustration der Addition von Punkten auf einer elliptischen Kurve: links erhält man die Summe von P und Q, indem man den eindeutig bestimmten Schnittpunkt der Geraden durch P und Q mit der Kurve schneidet (dies ist der Punkt -R) und ihn an der x-Achse spiegelt: P+Q=R. Ähnlich erhält man das Doppelte des Punktes P im rechten Bild: man schneidet die Tangente durch P mit der elliptischen Kurve und erhält den Punkt -R. Diesen spiegelt man wiederum an der x-Achse und erhält 2P=R.
|
Man kann die Gleichung E: y^2=x^3+ax+b statt im Reellen auch über einem endlichen Körper betrachten. Endliche Körper sind Körper mit einer endlichen Anzahl von Elementen, im Gegensatz zu Körpern wie den rationalen oder den reellen Zahlen, die unendlich viele Elemente besitzen. Bei endlichen Körpern, deren Elementezahl prim ist, spricht man von Primkörpern, und die Anzahl der Elemente von Primkörpern heißt auch Charakteristik. Elliptische Kurven über solchen Körpern haben die Eigenschaft, dass sie ebenfalls eine endliche Anzahl von Elementen haben. Ist die Charakteristik des Grundkörpers klein, so kann man die Anzahl einfach durch Abzählen bestimmen. Ab einer gewissen Größe ist dies jedoch nicht mehr praktikabel, so dass man auf spezielle Zählalgorithmen zurückgreifen muss. Die in meiner Diplomarbeit untersuchten Algorithmen (Schoof und SEA) sind Beispiele dafür. |
|
Der diskrete Logarithmus über der Punktegruppe einer elliptischen Kurve ist ein schwer lösbares Problem, das die Grundlage für kryptographische Anwendungen bildet. Gegeben sind zwei Punkte P und Q aus der Punktegruppe einer elliptischen Kurve, von denen man weiß, dass Q das k-te Vielfache von P ist, d.h. es gilt Q=kP. Gesucht ist nun der Faktor k. Ist die elliptische Kurve so gewählt, dass P aus einer Untergruppe der Kurve stammt, die eine hinreichend große Anzahl von Elementen hat, so ist das Finden dieses Faktors k eine sehr schwere Aufgabe, die für kryptographische Zwecke gut geeignet ist. Genau genommen ist bei einer gewissen Menge von Systemparametern exakt diese Zahl k der Private-Key in einem auf elliptischen Kurven basierenden Kryptosystem, und der Public-Key besteht aus den beiden Punkten P und Q. |